We begin by defining orthogonal sets and orthonormal sets. So, let
![]() be a subset of the space
be a subset of the space ![]() .
. ![]() is said to be orthogonal
if
is said to be orthogonal
if
![]() , if
, if ![]() , and it is said to be orthonormal is
, and it is said to be orthonormal is
![]() , where
, where
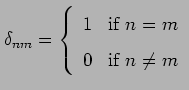
The set ![]() is said to be complete if its span is dense in
is said to be complete if its span is dense in
![]() . One can show that
. One can show that ![]() is complete if and only if the only
element orthogonal to
is complete if and only if the only
element orthogonal to ![]() is zero.
is zero.
The set ![]() is said to be a basis for the Hilbert space
is said to be a basis for the Hilbert space ![]() if for every
if for every ![]() , there exists a unique sequence of scalars
, there exists a unique sequence of scalars
![]() such that
such that
![]() . A basis
. A basis ![]() is said to be
orthonormal if it is orthogonal and
is said to be
orthonormal if it is orthogonal and ![]() , for all
, for all ![]() . It is
standard that if
. It is
standard that if ![]() is an orthonormal basis for
is an orthonormal basis for ![]() , then for all
, then for all
![]() , we have
, we have
and
Next, we define unconditional bases and Riesz bases.
Definition:
A basis ![]() for the Hilbert space
for the Hilbert space ![]() is called unconditional
if whenever
is called unconditional
if whenever
![]() ,
,
![]() .
.
Definition:
A subset ![]() of the Hilbert space
of the Hilbert space ![]() is called a Riesz basis
if there exists an orthonormal basis
is called a Riesz basis
if there exists an orthonormal basis ![]() for
for ![]() and an isomorphism
and an isomorphism
![]() , such that
, such that ![]() , for all
, for all ![]() .
.
Definition:
Let ![]() be a Hilbert space and let
be a Hilbert space and let ![]() and
and ![]() be subsets of
be subsets of
![]() . If
. If
![]() , then
, then ![]() and
and ![]() are
said to be quadratically close.
are
said to be quadratically close.