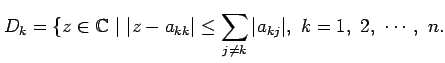: ¤³¤Îʸ½ñ¤Ë¤Ä¤¤¤Æ...
Remarks: Let  and
and  be
be
 matrices.
matrices.
- We said that if
 and
and  are similar, then they have the same
eigenvalues. In particular,
if
are similar, then they have the same
eigenvalues. In particular,
if  is diagonalizable, then
is diagonalizable, then  is similar to a diagonal matrix
is similar to a diagonal matrix  .
Thus,
.
Thus,  and
and  have the same eigenvalues
which means the diagonal elements of
have the same eigenvalues
which means the diagonal elements of  are the eigenvalues of
are the eigenvalues of  . Now
if
. Now
if  is diagonalizable, then there exists
a nonsingular matrix
is diagonalizable, then there exists
a nonsingular matrix  such that
such that
 . In this case, we say
. In this case, we say
 diagonalizes
diagonalizes  or
or  is diagonalizable
via
is diagonalizable
via  . Now after explaining the relationship between
. Now after explaining the relationship between  and
and  (they
have the same eigenvalues),
the questions that arise are:
(they
have the same eigenvalues),
the questions that arise are:
- What is the relationship between
 and
and  ?
?
- Are
 and
and  unique?
unique?
The answer to this first is that the columns of  are eigenvectors of
are eigenvectors of
 . The answer to the second is
. The answer to the second is  is not unique and
is not unique and  is not necessarily unique. In fact, if you multiply
is not necessarily unique. In fact, if you multiply
 by any nonzero number,
then the resulting matrix will diagonalize
by any nonzero number,
then the resulting matrix will diagonalize  .
Also, if you change the order of the columns of
.
Also, if you change the order of the columns of  , then the resulting
matrix will diagonalize
, then the resulting
matrix will diagonalize  . If you do so,
. If you do so,  also may change (will have the same elements as the original, but the
location of these elements may change),
which means
also may change (will have the same elements as the original, but the
location of these elements may change),
which means  is not necessarily unique.
is not necessarily unique.
Remark: To diagonalize an
 matrix
matrix  that has
that has  linearly independent eigenvectors,
find
linearly independent eigenvectors,
find  linearly independent eigenvectors
linearly independent eigenvectors  ,
,  ,
,  ,
,  ,
of
,
of  . Then form the
matrix
. Then form the
matrix
![$ P = [x_1 ~ x_2 ~ \cdots ~ x_n]$](img12.png) . Now
. Now
 , where
, where  is
a diagonal matrix whose
diagonal elements are the eigenvalues of
is
a diagonal matrix whose
diagonal elements are the eigenvalues of  corresponding to the
eigenvalues of
corresponding to the
eigenvalues of
 ,
,  ,
,  ,
,  .
.
- Now recall that the eigenvalues of Hermitian matrices and the
diagonal elements are real and the
eigenvalues of skew-Hermitian
matrices and the diagonal elements have zero real parts. Also, recall that
if
 is unitary, then
is unitary, then
 (note
(note
 can be complex),
can be complex),  is normal,
is normal,
 ,
,
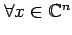 ,
and if
,
and if  is an eigenvalue of
is an eigenvalue of  , then
, then
 . Moreover,
any two distinct columns of
. Moreover,
any two distinct columns of  are orthogonal (i.e.
are orthogonal (i.e.
 , when
, when
 , and each one of them is a unit vector). Here are more facts
about these matrices:
, and each one of them is a unit vector). Here are more facts
about these matrices:
- (Schur's Theorem) If
 is an
is an
 matrix, then there
exists a unitary matrix
matrix, then there
exists a unitary matrix  such that
such that
 , where
, where  is upper-triangular. Moreover,
is upper-triangular. Moreover,  and
and  have the
same eigenvalues.
have the
same eigenvalues.
- From the above, note that we can write
 (proof:
exercise). This is called the Schur decomposition of
(proof:
exercise). This is called the Schur decomposition of  or
Schur normal form.
or
Schur normal form.
- From Schur's theorem: If
 is an
is an
 hermitian or a
skew-Hermitian matrix, then there
exists a unitary matrix
hermitian or a
skew-Hermitian matrix, then there
exists a unitary matrix  such that
such that
 , where
, where  is diagonal.
Thus,
is diagonal.
Thus,  is diagonalizable, and we say in this case
is diagonalizable, and we say in this case  is unitarily
diagonalizable.
is unitarily
diagonalizable.
Proof of the Hermitian Case: By Schur's Theorem, there exists a
unitary matrix  and an upper-triangular matrix
and an upper-triangular matrix  such that
such that
 . Now take the Hermitian transpose of both sides to get
. Now take the Hermitian transpose of both sides to get
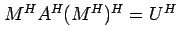 . Thus,
. Thus,
 . But,
. But,
 also. Therefore,
also. Therefore,  , which
implies
, which
implies  is diagonal. The skew-Herimitian case is
similar.
is diagonal. The skew-Herimitian case is
similar.
 in Schur's decomposition is diagonal iff
in Schur's decomposition is diagonal iff  is normal.
Moreover, when
is normal.
Moreover, when  is normal, the rows of
is normal, the rows of  are eigenvetors of
are eigenvetors of  . Thus,
. Thus,  is unitarily diagonalizable iff
is unitarily diagonalizable iff  is
normal. Moerover,
is
normal. Moerover,
 is normal iff
is normal iff  has a complete orthonormal set of eigenvectors.
has a complete orthonormal set of eigenvectors.
- From the previous part, if you take
 to be real symmetric, then
there
exists an orthogonal matrix
to be real symmetric, then
there
exists an orthogonal matrix  such that
such that
 , where
, where  is diagonal. Thus,
is diagonal. Thus,  is diagonalizable, and we
say in this case
is diagonalizable, and we
say in this case  is orthogonally
diagonalizable (proof: exercise). The eigenvalues of a real
symmetric matrix are real and eigenvectors are real.
Also, eigenvectors corresponding to different eigenvalues are orthogonal.
is orthogonally
diagonalizable (proof: exercise). The eigenvalues of a real
symmetric matrix are real and eigenvectors are real.
Also, eigenvectors corresponding to different eigenvalues are orthogonal.
- If
 is Herimitian, then eigenvectors that correspond to different
eigenvalues are orthogonal.
is Herimitian, then eigenvectors that correspond to different
eigenvalues are orthogonal.
Proof: Let
 and
and
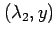 be two eigenpairs of
be two eigenpairs of
 where
where
 . We have to prove that
. We have to prove that 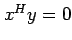 . Now
consider
. Now
consider
Therefore,
 , which implies
, which implies
 , .
Since
, .
Since
 , then
, then 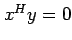 .
.
 is orthogonaly diagonalizable iff
is orthogonaly diagonalizable iff  has
has  orthonormal
eigenvectors iff
orthonormal
eigenvectors iff  is real symmetric.
is real symmetric.
- (Cayley-Hamilton Theorem) Every matrix satisfies its characteristic
equation.
Transforming Complex Hermitian Eigenvalue Problems to Real Ones
Let
 be a complex Hermitian matrix, where
be a complex Hermitian matrix, where  and
and  are
real
are
real
 matrices and let
matrices and let
 be an eigenpair of
be an eigenpair of  , where
, where 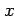 and
and  are in
are in
 (recall that
(recall that  is real because
is real because
 is Hermitian).
Now,
is Hermitian).
Now,
 if and
only if
if and
only if
Note that since  is Hermitian, then
is Hermitian, then  is symmetric and
is symmetric and  is
skew-symmetric. Hence,
the matrix
is
skew-symmetric. Hence,
the matrix
![$ \left[\begin{array}{cc}
A & -B\\
B & A\end{array}\right]$](img46.png) is real symmetric. Thus, we managed to reduce a complex Hermitian
eigenvalue problem of order
is real symmetric. Thus, we managed to reduce a complex Hermitian
eigenvalue problem of order  to a real symmetric eigenvalue
problem of order
to a real symmetric eigenvalue
problem of order  .
.
The companion Matrix
Let  be the
be the
 matrix such that
matrix such that
 ,
,
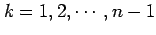 , and
, and
 ,
,
 . By expanding the determinant of
. By expanding the determinant of
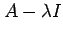 across the
last row, you'll find out that the characterestic polynomial of
across the
last row, you'll find out that the characterestic polynomial of  is
is
The matrix  is called the companion matrix of the polynomial
is called the companion matrix of the polynomial
 . The companion matrix is sometimes
defined to be the traspose of the matrix above and it satisfies the
following:
. The companion matrix is sometimes
defined to be the traspose of the matrix above and it satisfies the
following:
 ,
,
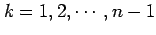 ,
and
,
and
![$ Ae_n = [-c_0 ~ -c_1 ~ \cdots ~ -c_{n-1}]^T$](img56.png) .
.
Definition: The spectral radius of an
 matrix
matrix  ,
denoted
,
denoted 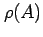 ,
is the maximum eigenvalue of
,
is the maximum eigenvalue of  in magnitude;
i.e. if the eigenvalues of
in magnitude;
i.e. if the eigenvalues of  are
are
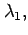
 ,
,  ,
,
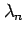 , then
, then
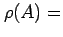 max
max .
.
Definition: Let  be an
be an
 matrix and let
matrix and let  be the
matrix such that
be the
matrix such that
 .
.
- The one-norm of
 , denoted
, denoted 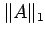 , is the maximum column sum of
, is the maximum column sum of
 .
.
- The
 -norm, denoted
-norm, denoted
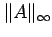 , of
, of  is the maximum
rwo sum of
is the maximum
rwo sum of  .
.
- The two-norm (or spectral norm) of
 , denoted
, denoted  , is the
non-negative square root of
, is the
non-negative square root of
 .
Note that
.
Note that 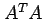 is square and symmetric.
is square and symmetric.
- The Frobenius norm of
 , denoted
, denoted 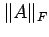 , is
, is
 .
.
Remark: There are properties and equivalent definitions for matrix
norms, but we don't have time
to go over that.
Theorem (Gerschgorin): Let  be an
be an
 matrix and define
the disks
matrix and define
the disks
If  is an eigenvalue of
is an eigenvalue of  , then
, then  is located in
is located in
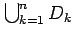 .
.



: ¤³¤Îʸ½ñ¤Ë¤Ä¤¤¤Æ...
Iyad Abu-Jeib
Ê¿À®17ǯ1·î1Æü
![]() and
and ![]() be
be
![]() matrices.
matrices.
![]() are eigenvectors of
are eigenvectors of
![]() . The answer to the second is
. The answer to the second is ![]() is not unique and
is not unique and ![]() is not necessarily unique. In fact, if you multiply
is not necessarily unique. In fact, if you multiply
![]() by any nonzero number,
then the resulting matrix will diagonalize
by any nonzero number,
then the resulting matrix will diagonalize ![]() .
Also, if you change the order of the columns of
.
Also, if you change the order of the columns of ![]() , then the resulting
matrix will diagonalize
, then the resulting
matrix will diagonalize ![]() . If you do so,
. If you do so, ![]() also may change (will have the same elements as the original, but the
location of these elements may change),
which means
also may change (will have the same elements as the original, but the
location of these elements may change),
which means ![]() is not necessarily unique.
is not necessarily unique.
![]() matrix
matrix ![]() that has
that has ![]() linearly independent eigenvectors,
find
linearly independent eigenvectors,
find ![]() linearly independent eigenvectors
linearly independent eigenvectors ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
of
,
of ![]() . Then form the
matrix
. Then form the
matrix
![]() . Now
. Now
![]() , where
, where ![]() is
a diagonal matrix whose
diagonal elements are the eigenvalues of
is
a diagonal matrix whose
diagonal elements are the eigenvalues of ![]() corresponding to the
eigenvalues of
corresponding to the
eigenvalues of
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
![]() and an upper-triangular matrix
and an upper-triangular matrix ![]() such that
such that
![]() . Now take the Hermitian transpose of both sides to get
. Now take the Hermitian transpose of both sides to get
![]() . Thus,
. Thus,
![]() . But,
. But,
![]() also. Therefore,
also. Therefore, ![]() , which
implies
, which
implies ![]() is diagonal. The skew-Herimitian case is
similar.
is diagonal. The skew-Herimitian case is
similar.
![]() and
and
![]() be two eigenpairs of
be two eigenpairs of
![]() where
where
![]() . We have to prove that
. We have to prove that ![]() . Now
consider
. Now
consider
![]() be a complex Hermitian matrix, where
be a complex Hermitian matrix, where ![]() and
and ![]() are
real
are
real
![]() matrices and let
matrices and let
![]() be an eigenpair of
be an eigenpair of ![]() , where
, where ![]() and
and ![]() are in
are in
![]() (recall that
(recall that ![]() is real because
is real because
![]() is Hermitian).
Now,
is Hermitian).
Now,
![]() if and
only if
if and
only if
![$\displaystyle \left[\begin{array}{cc}
A & -B\\
B & A\end{array}\right]\left[\b...
...\
y\end{array}\right]=\lambda \left[\begin{array}{c}
x\\
y\end{array}\right].$](img45.png)
![]() is Hermitian, then
is Hermitian, then ![]() is symmetric and
is symmetric and ![]() is
skew-symmetric. Hence,
the matrix
is
skew-symmetric. Hence,
the matrix
![$ \left[\begin{array}{cc}
A & -B\\
B & A\end{array}\right]$](img46.png) is real symmetric. Thus, we managed to reduce a complex Hermitian
eigenvalue problem of order
is real symmetric. Thus, we managed to reduce a complex Hermitian
eigenvalue problem of order ![]() to a real symmetric eigenvalue
problem of order
to a real symmetric eigenvalue
problem of order ![]() .
.
![]() be the
be the
![]() matrix such that
matrix such that
![]() ,
,
![]() , and
, and
![]() ,
,
![]() . By expanding the determinant of
. By expanding the determinant of
![]() across the
last row, you'll find out that the characterestic polynomial of
across the
last row, you'll find out that the characterestic polynomial of ![]() is
is

![]() matrix
matrix ![]() ,
denoted
,
denoted ![]() ,
is the maximum eigenvalue of
,
is the maximum eigenvalue of ![]() in magnitude;
i.e. if the eigenvalues of
in magnitude;
i.e. if the eigenvalues of ![]() are
are
![]()
![]() ,
, ![]() ,
,
![]() , then
, then
![]() max
max![]() .
.
![]() be an
be an
![]() matrix and let
matrix and let ![]() be the
matrix such that
be the
matrix such that
![]() .
.
 .
.
![]() be an
be an
![]() matrix and define
the disks
matrix and define
the disks