Definition: The sinc
function is defined to be:
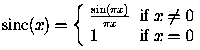
Definition: Sinc methods are a family
of formulas based on the sinc function which give accurate
approximations of derivatives and definite and indefinite integrals and
convolutions. These methods were developed by Frank Stenger.
One of the nice properties of these methods is that they can handle
boundary layer problems, integrals with infinite intervals or with
singular integrands, and ODEs or PDEs that have coefficients with
singularities.
Definition: The matrix
I(-1) is defined as follows

This matrix is used for sinc quadrature and sinc
convolution.
Notice that the above matrix can be written as a sum of two matrices;
one of them is the matrix [0.5] which is of rank 1, and the other is real
skew-symmetric Toeplitz.
Another important matrix in Sinc methods is I(1). This
is a skew-symmetric Toeplitz matrix generated by the function
f(x)=-ix on [-Pi,Pi]. Thus, if b is an eigenvalue of
I(1), then b=ia, where a is a real number
greater than or equal to -Pi and less than or equal to Pi.
The n by n I(1) is defined as follows
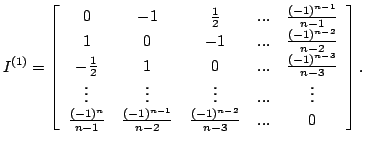
|